问题：
Q1《高考数学（文科）小卷实战基础60套》 ： 小卷实战20/7 为什么是直线与抛物线相切
 
Q2《高考数学（文科）小卷实战基础60套》 ： 小卷实战20/12 最后一步看不懂
 
Q3《高考数学（文科）小卷实战基础60套》 ： 小卷实战20/14 方程怎么设
 
Q4《高考数学（文科）小卷实战基础60套》 ： 小卷实战23/8 为什么X0＝p
 

考点说明：Q1： 线性规划
 
Q2：函数与方程，三角函数的恒等变换
 
Q3：双曲线的定义与标准方程
 
Q4：抛物线的定义
 
问题解答：Q1：由题意知抛物线的方程为y=x2/z，当抛物线的开口越小，z就越小，当抛物线的开口越大，z就越大，所以由平面区域和抛物线的图知当抛物线与直线y=x-1相切的时候，抛物线的开口最小，此时z才能取得最小值.
 
Q2：最后一步：tanβ=β，故tan(β+)==.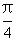
 
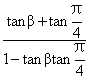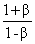Q3：由题意易知双曲线有两种情况，分别为焦点在x轴上和焦点在y轴上。当焦点在x轴上时，通常双曲线方程可设为x2/a2-y2/b2=1，其渐近线方程为y=±bx/a，由题意b/a=1/2，设b=λ，则a=2λ，所以双曲线方程可设为x2/4λ2-y2/λ2=1，同理当焦点在y轴上也可用同样的方法。
 
Q4：由抛物线的定义有点M到准线的距离为x0+p/2=|MF|，由圆的定义知|MA|=x0，故|AF|=p/2，再由条件得|MA|/|AF|=2得x0=2·p/2=p.
 
编辑提点：Q1：理解抛物线y=ax2（a≠0）的开口大小和a的关系。
 
Q2：要熟练掌握三角函数的恒等变换公式。
 
Q3：正确理解抛物线的方程与渐近线方程的关系。
 
Q4：正确理解抛物线的定义。